Softening Edges: Chaikin’s Algorithm in Generative Art

In many of my generative sketches, I start with raw geometry: a jagged polygon, a noisy perimeter, or just a random set of coordinates. These tend to feel too rigid, too mechanical… too sharp. What I often want instead is a way to soften that geometry, to make it feel more fluid, more organic. One of my favourite ways to do this is by applying a few iterations of Chaikin’s corner-cutting algorithm. I used it heavily in my series WAVETABLE: four fucked waveforms (2024):

WAVETABLE

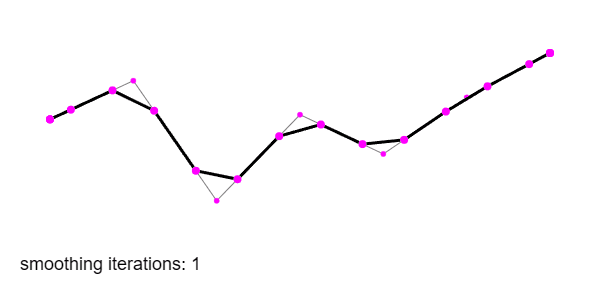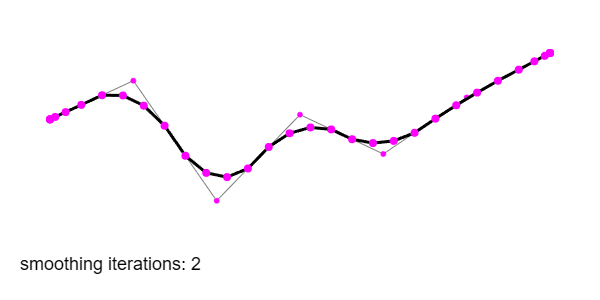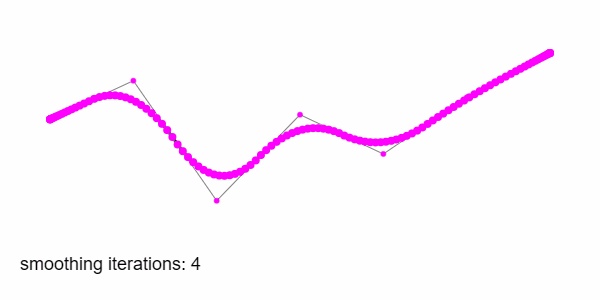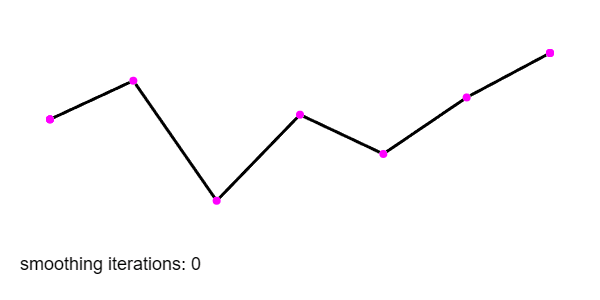
Chaikin’s method is simple: it smooths a path by iteratively “cutting corners” by a set ratio. For each pair of points, it inserts two new ones slightly closer to each end, then repeats the process as many times as needed. The result is a sequence of points that approximate a smooth curve, without needing to touch splines, control handles, or Bézier maths.

How It Works

Given a set of points for a polyline or polygon:

  1. For each pair of consecutive points (A, B) of a segment, calculate:
    • Q = 0.75 * A + 0.25 * B
    • R = 0.25 * A + 0.75 * B
  2. Replace the original segment with the new points Q and R.
  3. Repeat for a few iterations.

This gradually rounds sharp corners, and after several iterations the shape converges toward a quadratic B-spline. The resulting form is still defined entirely by your original path—just softened.

chaikin demo

Code example

Here’s an implementation I use in my chaikin-curve repo:

function chaikin(point_array, n_iterations) { // point_array is a set of x,y coords
  let smooth_array = [];
  for (let iter = 0; iter < n_iterations; iter++) {
    let temp = [];
    for (let i = 0; i < point_array.length - 1; i++) {
      let p0 = [point_array[i][0], point_array[i][1]]; // segment start
      let p1 = [point_array[i + 1][0], point_array[i + 1][1]]; // segment end
      let q = [0.75 * p0[0] + 0.25 * p1[0], 0.75 * p0[1] + 0.25 * p1[1]];
      let r = [0.25 * p0[0] + 0.75 * p1[0], 0.25 * p0[1] + 0.75 * p1[1]];
      temp.push(q);
      temp.push(r);
    }
    point_array = temp.slice();
  }

  // then add back in start and end points
  point_array.splice(0, 0, [points[0][0], points[0][1]]);
  point_array.push([
    points[points.length - 1][0],
    points[points.length - 1][1],
  ]);
  return point_array;
}

Why Not Just Use Bézier Curves?

A fair question. Libraries like p5.js give you Bézier curves and curveVertex() for free. So why reach for Chaikin?

Chaikin’ corner cutting doesn’t require precise control or knowledge of Béziers. It works with whatever geometry you give it. No need to think about angles and control points. It’s ideal for softening the edges of generative shapes — messy blobs, grid-based forms, even text outlines — where the goal is aesthetic rather than mathematical precision.

Sure, curve() might give me an equally good result in most cases, but having a more custom solution is handy sometimes.

SigHack’s excellent post on Chaikin curves (in Processing) gives some really nice use cases: from softened voronoi cells, to brush strokes.

Chaikin’s algorithm won’t replace Bézier curves and splines, but it’s an excellent tool to keep around when you’re working procedurally and want a bit of softness.